הגדרת גיאומטריה
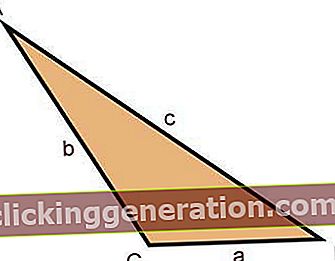
ה גֵאוֹמֶטרִיָה זה אחד מענפי המתמטיקה העוסק בחקר תכונות החלל כגון: נקודות, מישורים, מצולעים, קווים, פולידרות, עקומות, משטחים, בין היתר.
בין המטרות השונות שמקורן רחוק במצרים העתיקה הן: פתרון בעיות הקשורות למדידות, כגון הצדקה תיאורטית של אלמנטים מדידה כגון מצפן, פנטוגרף ותאודוליט.
אם כי גם עם הזמן ובזכות ההתקדמות שהושגה במחקר שלו, הגיאומטריה כיום זהו היסוד התיאורטי של נושאים אחרים כגון מערכת המיקום הגלובלית, יותר מכל כאשר זה בשילוב עם ניתוח מתמטי ומשוואות דיפרנציאליות וזה גם שימושי מאוד וייעוץ בהכנת עיצובים כגון רישום טכני או עבור הרכבת עבודות יד.
כפי שאמרנו לעיל לידתו של משמעת זו מתחילה במצרים העתיקה, הגיאומטריה הקלאסית המבוססת על אקסיומות ששררו באותם הימים השתמשו במצפן ובסרגל כדי לחקור את הקונסטרוקציות השונות.
מכיוון שהגיאומטריה אינה מתקבלת על הדעת על טעויות, כך פותחו המערכות האקסיומטיות שהציעו ירידה בשגיאה והנחילו שיטה קפדנית ביותר. המערכת האקסיומטית הראשונה הגיעה מכיוון שלא הייתה יכולה להיות אחרת עם מי שנחשב כיום אבי הגיאומטריה, המתמטיקאי היווני אוקלידס.
עבודתו "היסודות" מרכיבה את תורתו בעולם האקדמי של אותה תקופה והיא אחת היצירות הידועות ביותר וזו שנתנה לעולם את מירב הפניות.
בכך, אוקלידס, מעלה כמה פוסטולטים ומשפטים שתקפים עד היום בחינוך הבית ספרי, כל כך הרבה מכם, אם לא הייתם נרדמים בשעות הגיאומטריה תוכלו לזהות אותם.
אז מה שנצטט להלן ושכמה מכירים יזהו, אנו חייבים זאת אך ורק לאוקליד: עבור שתי נקודות ניתן לצייר קו ישר בלבד, כל קטע ישר יכול להאריך ללא הגבלת זמן, כל הזוויות הנכונות שוות, סכום זוויות פנים של כל משולש שוות ל -180 מעלות ובמשולש ימין ריבוע ההיפוטנוזה שווה לסכום ריבועי הרגליים ואנחנו יכולים להמשיך, אך איננו רוצים להדגיש את המורה לגיאומטריה.
