הגדרת משוואה
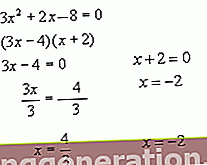במתמטיקה, השוויון בין שני ביטויים אלגבריים נקרא משוואה, שתיקרא חברי המשוואה. במשוואות, הם יופיעו קשורים באמצעות פעולות מתמטיות, מספרים ואותיות (לא ידועים).
רוב הבעיות המתמטיות מוצאות את התנאים שלהן לידי ביטוי בצורה של משוואה אחת או יותר.
בינתיים, כאשר כל אחד מערכי המשתנים במשוואה עומד בשוויון, מצב זה ייקרא פיתרון המשוואה.
לפני משוואה יכולים להתרחש התרחישים הבאים, שאף אחד מהערכים של הלא נודע אינו מגיע לשוויון, או להיפך, שכל ערך אפשרי של הלא נודע ממלא אותו, במקרה זה אנו עומדים בפני מה שמכונה זהויות ב במתמטיקה וכששני ביטויים מתמטיים חופפים באי-השוויון, זה ייקבע כאי-שוויון.
ישנם סוגים שונים של משוואות, ביניהם, אנו מוצאים את המשוואה הפונקציונלית, שהיא קבוצה בה הקבועים והמשתנים המעורבים אינם מספרים אמיתיים אלא פונקציות. כאשר מופיע חלק מהמרכיבים מפעיל דיפרנציאלי, הם נקראים משוואות דיפרנציאליות. ואז יש את משוואת הפולינום, שהיא זו שקובעת את השוויון בין שני פולינומים. מצד שני, משוואות מדרגה ראשונה הן אלו בהן המשתנה x אינו מועלה לשום כוח, כאשר 1 הוא המעריך שלו. בינתיים, המאפיין האופייני והדיפרנציאלי של משוואות המכונות משוואות מדרגה שניה הוא שיהיו לה שני פתרונות אפשריים לכך.
אבל באסטרונומיה, שם המונח אומר גם הווה, משוואה היא ההבדל בין המקום או התנועה הממוצעת לבין האמיתי או הנראה שיש לכוכב.
