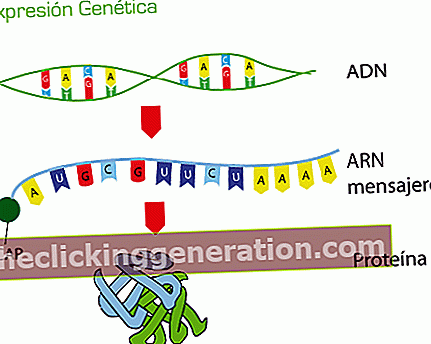
הגדרת משולש
הידוע כאחת הדמויות הגיאומטריות הפשוטות והנפוצות ביותר, ניתן לתאר את המשולש כדמות עם שלושה צלעות המצטרפות יחד ויוצרות שלוש קודקודים או פינות (ומכאן שמו של תלת-זווית) ושהן גם סופיות מקודקוד עד האחר. בכך שהוא מכיל את הצדדים בצורה של מקטעים שאינם מיושרים במקביל, המשולש נחשב מצולע. שם המשולש מוחל באופן ספציפי על משולשים בעלי משטח ישר, כלומר ללא נפח, מכיוון שאלה שיש להם מקבלים אז גרסאות של אותו שם. המשולש מיוצג על ידי סימבולוגיית ABC (כל אות מייצגת צד אחד).
ישנם כמה אלמנטים ספציפיים של המשולש והם חיוניים לצורתו, וכן חשוב להגדיר את המאפיינים העיקריים של דמות זו. במובן זה, אחד האלמנטים הראשונים שיש לקחת בחשבון הוא העובדה שסכום הזוויות הפנימיות של משולש נמדד תמיד 180 °. לכן, הזוויות החיצוניות של המשולש תמיד משלימות לזווית הפנימית מכיוון ששניהם יחד חייבים ליצור 180 °. יחד עם זאת, הזווית החיצונית של כל אחד מהקודקודים שווה לסכום הזוויות שאינן סמוכות אליו, ואילו סכום שלוש הזוויות החיצוניות חייב להסתכם ב -360 מעלות.
ניתן לארגן משולשים על פי צורתם וכן על פי סוג הזוויות הנוצרות בתוכו. במקרה הראשון יש לנו שלושה סוגים של משולשים: שְׁוֵה צְלָעוֹת (שצדדיו שווים ומכילים את אותו אורך), המשולש שְׁוֵה שׁוֹקַיִם (שיש לו שני צדדים באותו אורך וקטן יותר, בנוסף לעובדה ששתי הזוויות של קטע קטן יותר זהות) ולבסוף סקלנה (שיש בו כל הצדדים באורכים שונים ובזוויות שונות).
מצד שני, אם ניקח בחשבון את סוגי הזוויות של המשולש, נוכל להגדיר אותו כ משולש ישר זווית (עם זווית של 90 °, שתי רגליים והיפוטנוזה), משולשים קהים (עם זווית גדולה מ 90 °), משולש חריף (עם שלוש זוויות פחות מ 90 °) ולבסוף, ה משולש שקול (זו שיש לה שלוש זוויות פנימיות של 90 °).
