הגדרת זהויות טריגונומטריות
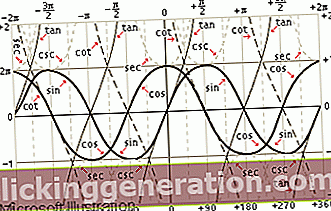המושג זהויות טריגונומטריות הוא מושג המשמש בתחום המתמטיקה בכדי להתייחס לפונקציות הטריגונומטריות המשתנות שניתן למצוא באיור גיאומטרי. טריגונומטריה היא הענף של המתמטיקה המתמחה בניתוח ולימוד משולשים, במיוחד בצורות, במשמעויות ובערכים של הזוויות השונות העשויות להתקיים. הזהויות הטריגונומטריות יהיו אז תוצאה של אותם ערכים המשתנים ומגוונים מאוד זה מזה.
כמו במרכיבים רבים במתמטיקה, המושגים היו קיימים עוד מימי קדם בהם פילוסופים יוונים כבר ביססו את מושגי הפונקציות והערכים של זוויות הדמויות הגיאומטריות. מושגים אלה ישופרו רק במודרניות, במאה השבע עשרה, כאשר צוינו באופן אלגברי כמסוגלים לבצע כל מיני חישובים בין הזוויות השונות.
זהות טריגונומטרית ניתנת להגדרה רחבה ככל משתני הזווית האפשריים שיכולים להתקיים באיור גיאומטרי. זהויות אלה מיוצגות תמיד מהאותיות היווניות כגון אלפא, בטא, אומגה וכו '. אלמנטים כמו מעלות צלזיוס משמשים גם לקביעת המשתנים של כל זהות. הידועים ביותר הם אלה שנוצרו בין סינוס לקוסינוס, סינוס ומשיק וכו '. זהויות טריגונומטריות הן צורות פשוטות המאפשרות לנו לבצע ולדעת את הפונקציות השונות של הטריגונומטריה. כל השאלות הללו של המתמטיקה, ליתר דיוק של טריגונומטריה, משמשות לארגון החישובים השונים שיש לבצע מתוך הפונקציות הספציפיות של כל סוג נתונים. זהויות טריגונומטריות משתנות מאוד ומאפשרות לקבל אפשרויות שונות לייצג כל פונקציה טריגונומטרית (כלומר הערכים) בדרכים מגוונות וספציפיות בהתאם לכל מקרה.
