הגדרת משפט
משפטים הם הצורך והדאגה המיוחדת של המתמטיקה וכשמדברים עליהם מתייחסים ההצהרות שניתן להוכיח שהן נכונות במסגרת הגיונית.
באופן כללי, המשפטים הם מורכב ממספר תנאים שניתן לרשום או לצפות מראש אליהם הם נקראים תגובות. בעקבות אלה תופיע המסקנה או האמירה המתמטית, שברור שתמיד תהיה נכונה בתנאי העבודה הנדונה, כלומר קודם כל בתוכן האינפורמטיבי של המשפט, מה שיתבסס הוא הקשר הקיים בין ההשערה והתיזה או השלמת העבודה.
אבל יש משהו בלתי נמנע למתמטיקה כאשר אמירה מסוימת סבירה להפוך למשפט והיא שהיא חייבת להיות מעניינת מספיק בתוך הקהילה המתמטית ולמען הקהל, אחרת ולמרבה הצער, זה יכול פשוט להיות מוטו, מסקנה או פשוט הצעה , לעולם לא להיות מסוגל להפוך למשפט.
וכדי להבהיר את הנושא מעט יותר, יש גם להבחין בין המושגים שהזכרנו לעיל, כך שאפילו אם איננו חלק מקהילה מתמטית, נוכל לזהות מתי מדובר במשפט, בלמה, מסקנה או הצעה.
למה היא הצעה, כן, אבל היא חלק ממשפט ארוך יותר. המסקנה מצידה היא אמירה העוקבת אחר משפט ולבסוף ההצעה היא תוצאה שאינה קשורה למשפט מסוים.
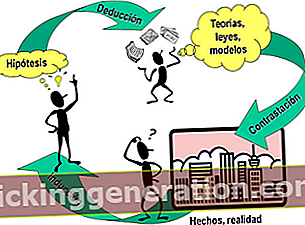
בתחילת הדרך ציינו כי משפט הוא משפט שניתן להוכיח רק במסגרת לוגית, ואילו עם מסגרת לוגית אנו מתייחסים למערכת אקסיומות או מערכת אקסיומטית ותהליך הסקה שיאפשר לנו להפיק משפטים מתוך אקסיומות ומשפטים שכבר נגזרו בעבר.
מצד שני, הרצף הסופי של נוסחאות לוגיות מעוצבות ייקרא הוכחה למשפט זה.
אמנם לא עם תשומת הלב המיוחדת שמקדישה המתמטיקה למשפטים, אך תחומים כמו פיזיקה או כלכלה מייצרים בדרך כלל אמירות שנגזרות מאחרים ונקראות גם משפטים.
